
可爱奶龙,带到班后就被虐待了,现在失踪了/ll
竞赛图(Tournament)的定义
对于一个任意两点恰有一条边的有向图称为「竞赛图」。
由于边集恰好描述了两两点之间的关系,可以视作「输赢」,故称之为「竞赛图」。
竞赛图的一些性质
1. 缩点后呈链状
注意,这里的「链状」不代表是一条链。
考虑缩点后任一点起做拓扑排序,对于不在同一强连通分量的两点 $u,v$,假设 $u$ 的拓扑序先于 $v$,必然存在边 $u\to v$。
将形成公差为 $1$ 的拓扑序形成的作为主链,支链为存在拓扑序差更大的边。如下图,就是缩点后竞赛图的一个示例。
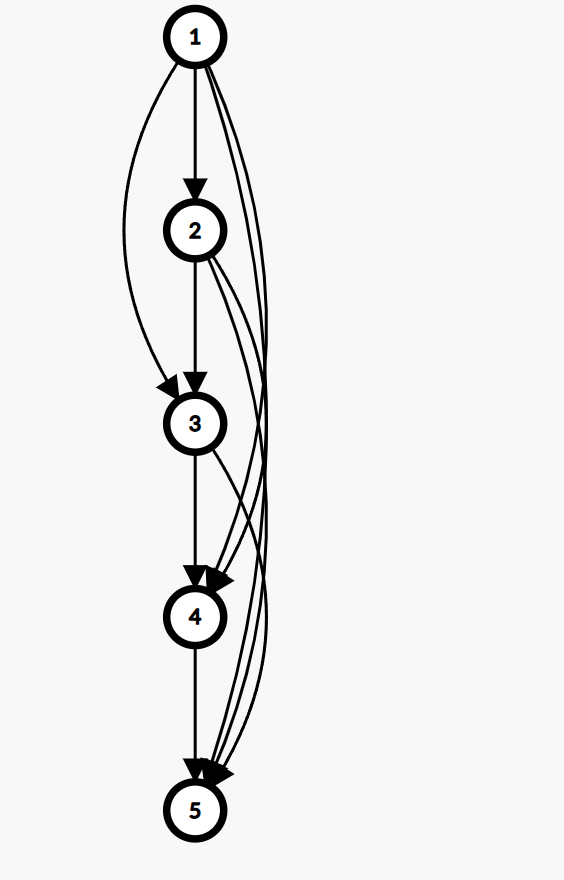
2. Camion-Moon 定理
强连通竞赛图一定有 Hamilton 回路。换句话说,竞赛图的一个强连通分量内有 Hamilton 回路。
考虑归纳,$n=1$ 显然正确。在 $n>1$ 时,假设 $n-1$ 已经形成 Hamilton 回路。由于 $n$ 加入后仍强连通,说明至少存在一对 $(u,v)$ 使得有边 $u\to n,n\to v$。插入即可,由于回路的结构,这显然仍呈回路。
3. Reidi 定理
竞赛图一定有 Hamilton 路径。
先缩点,然后用性质 2 找到一条 Hamilton 回路,再在通向下一个强连通分量点后断裂,形成 Hamilton 路径。顺次相接,即可找到一条 Hamilton 路径。
4. 不小于 $3$ 的 SCC 中必然存在三元环
考虑归纳,$n=3$ 时显然。$n>3$ 时,存在 Hamilton 通路 $1\to 2\to3\to\cdots\to n$(不一定是点的原始编号)。若存在 $3\to 1$,就结束了。不存在,说明有 $1\to 3$。把 $2$ 去掉,如此转化为 $n-1$ 的情况。由于 $n-1$ 存在,则此情况必然存在。
5. Landau 定理
给定不降的非负整数序列 $p$,使 $\sum\limits_{i=1}^np_i=\dbinom n2$。存在竞赛图使得节点出度为 $p_1,p_2,\cdots,p_n$ 的充要条件为:$\forall i\in[1,n],\sum\limits_{j=1}^ip_j\ge\dbinom i2$。
若对于任意 $i\in[1,n-1]$,都有 $\sum\limits_{j=1}^i p_i>\dbinom i2$,当且仅当该竞赛图强连通。
必要性:显然。
充分性:考虑调整法。找出一个出度序列为 ${0,1,\cdots,n-1}$ 的 $n$ 阶竞赛图,显然可以构造。每次找位置最靠前的 $a_x<p_x$,在找最小的 $a_y>p_y$。二者求和相同,故 $y>x$。故 $a_y>p_y\ge p_x>a_x$,于是 $a_y\ge a_x+2$。差为 $2$,则必然存在边 $y\to i,i\to x$,反向即可实现 $a_x\gets a_x+1,a_y\gets a_y-1$。如此调整,易使 $a=p$。
例题
P3561 [POI 2017] Turysta
给出竞赛图,求从每个点出发最长的不重点路径。$n\le2000$。
竞赛图中的强连通分量内必然有 Hamilton 回路,从每个点所在强连通分量内开始,按照拓扑序向后找回路即可,任意一个点都可直接到达下一个 SCC。难点在于构造方案。
CF1268D Invertation in Tournament
给出竞赛图,可以选择任意个点,使与该点相连的边方向翻转。求在使其变成强连通图的翻转最少次数,以及在此前提下的合法方案数。$n\le 2000$。
考虑原图形成的强连通分量数,假设有 $k$ 个。拓扑排序后,按照拓扑序从小到大排序,称第 $i$ 小的为「第 $i$ 强连通分量」。
$k=1$
无需操作,答案为 0 1。
$k\ge 3$
显然只要取第 $i\in[2,k-1]$ 强连通分量中任意一点取反即可。
$k=2$
引理:大小为 $n\ge 4$ 的强连通竞赛图中,必然存在大小为 $n-1$ 的强连通竞赛子图。
证明:考虑 Camion-Moon 定理,该强连通竞赛图存在 $n$ 阶 Hamilton 回路。设回路为 $p_1\to p_2\to\cdots\to p_n\to p_1$,把 $p_1$ 从该图中删掉,形成的是 $p_2\to\cdots\to p_n$ 的 Hamilton 路径。讨论剩下形成的强连通分量(注意,竞赛图中不存在大小为 $2$ 的强连通分量)。
- 若存在 $k\ge 3$ 的强连通分量。此强连通分量中存在 Hamilton 回路,选长度 $k-1$ 的路径,接上 $p_1$ 即可形成 $n-1$ 的强连通竞赛子图。
- 若大小全为 $1$。只需删除非头尾的强连通分量,然后接上 $p_1$ 即可。
综上,无论何种情况,都可构造出大小为 $n-1$ 的强连通竞赛子图。
根据如上引理,可将大小 $n\ge 4$ 的强连通分量划分成大小分别为 $n-1$ 与 $1$ 的连通分量,只需翻转大小为 $1$ 的点即可。
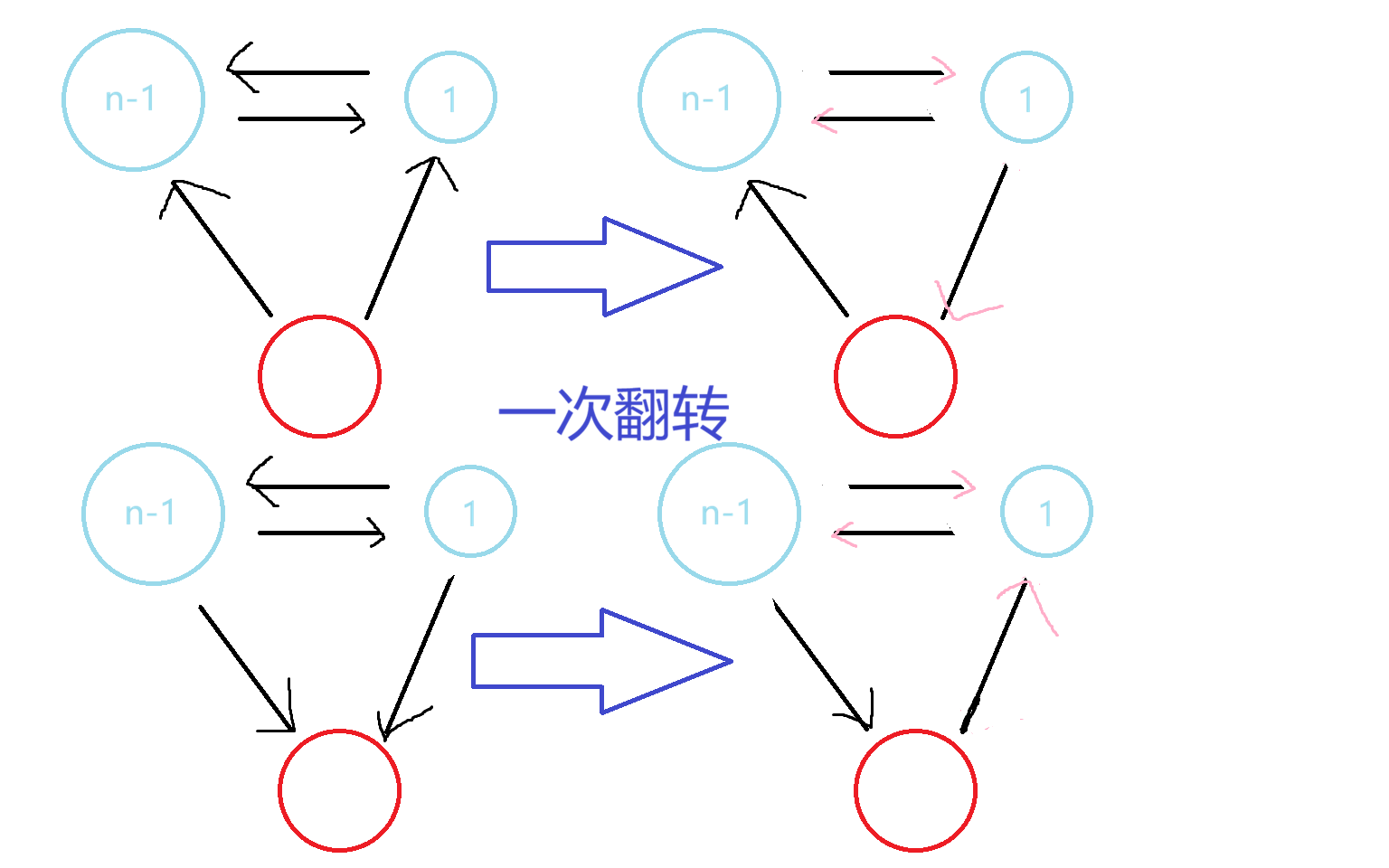
然后对每个点都判一遍是否可行,这部分可以用 Landau 定理解决,复杂度为 $\mathcal O(n^2\log n)$。
Landau 定理:设 $p_i$ 为竞赛图的出度序列,从小到大排序后,若对于任意 $i\in[1,n-1]$,都有 $\sum\limits_{j=1}^i p_i>\dbinom i2$,当且仅当该竞赛图强连通。
剩余的情况只有 $k=2$ 且 $n\le 6$,这部分很少,直接暴力枚举即可。