
玩原神玩的。
一些对 FHQ Treap 的简单介绍。
二叉搜索树
在动态进行区间操作时,常常需要数据结构来优化类似 $\mathcal O(n^2)$ 的时间复杂度,二叉搜索树 是一种优化复杂度的数据结构,定义如下:
- 二叉搜索树是一颗二叉树。
- 对于一个节点 $R$,若存在左子树,则 $R$ 的左子树所有点均小于 $R$ 的权值;若存在右子树,则 $R$ 的右子树的权值均大于 $R$ 的权值。
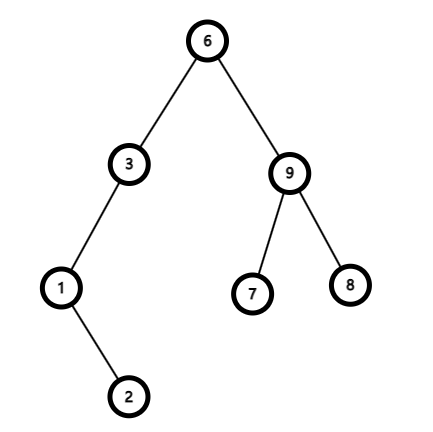
一棵二叉搜索树的示例
在进行动态查询操作时,显然操作的复杂度取决于树高。期望高度为 $\mathcal O(\log n)$,最劣情况为 $\mathcal O(n)$。故下介绍一种维护二叉搜索树的一种方式。
Treap
Treap,顾名思义,“树堆”。意即采用类似堆的性质来维护整棵二叉搜索树。 每个节点具有其权值 $val$,以及优先级 $rd$。其中权值满足二叉搜索树性质,优先级满足堆的性质。
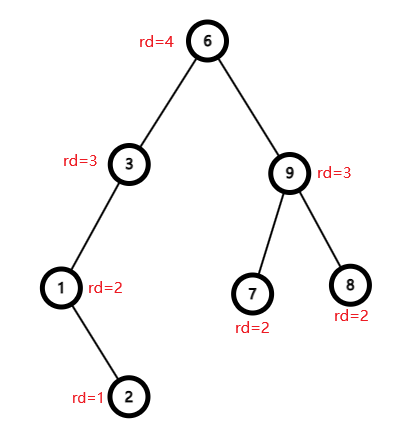
上图的优先级标注
然而问题便在于如何给节点的优先级赋值来达到期望的树高 $\mathcal O(\log n)$。 如若直接按照权值大小之类赋值,那么极易用一段有序的数据将树高卡为 $\mathcal O(n)$, 因此我们给所有点的优先级 随机赋值 来达到较为平衡的状态,那整个树的维护便得心应手了。
Treap 有两种实现方式,一种是 有旋Treap 一种是 无旋Treap(FHQ-treap)。
FHQ-Treap
FHQ-Treap 以其易懂、简洁、高效等优势而闻名,支持可持久化、维护序列等操作,由国家队成员范浩强提出。
基本操作
- 新建节点
|
|
- 更新节点信息
|
|
当然,如若这个节点还有其他信息,亦在此进行更新.
FHQ-Treap 的核心操作是 分裂(split) 与 合并(merge),通过这两个操作可以实现许多功能。下给出两种操作的具体步骤。
分裂
- 按值分裂 不妨设当前以 $v$ 为值进行分裂,那么整棵树 $T$ 将会分为所有 $val_p\le v$ 的子树 $T_x$ 以及所有 $val_p>v$ 的子树 $T_y$。设当前树的根节点为 $R$,那么根据二叉搜索树的性质,若 $val[R]\le v$,则 $T_y$ 必在其右子树上,而 $T_x$ 可以暂时认为当前即为 $R$,反之亦然。这样递归的进行下去,便将一棵树分裂成两棵。 代码如下:
|
|
- 按大小分裂 与上种方式类似,常用于进行 区间操作。设当前递归的树的根节点为 $R$,要分裂出 大小为 $len$ 的树为 $T_x$,剩下的树为 $T_y$。若 $sz[ls_R]\ge len$,那么 $T_x$ 必在 $R$ 的左子树上,同样的,$T_y$ 可以暂时的认为是 $R$,向 $ls_R$ 递归下去。 代码如下:
|
|
合并
对于两棵平衡树 $T_x$ 以及 $T_y$,合并的前提条件是:$\forall i\in T_x,\forall j\in T_y$ 都满足 $val_i\le val_j$. 考虑当前要合并的两点为 $i$,$j$。在 Treap 的定义中,我们知道树的结构要满足 堆 的性质,引入了 优先级 $rd$,这种参数就是为合并操作服务的。 若 $rd_i>rd_j$,那么 $i$ 为 $j$ 的父节点,由于 $val_i<val_j$,故保持 $i$ 节点的左子树不变,修改其右子树。形式化的,$rs(i)\gets \operatorname{merge}(rs_i,j)$,其中 $\operatorname {merge}$ 函数返回的是最终合并树的根节点。反之亦然。 代码如下:
|
|
普通平衡树
实现以下操作即可:
- 插入操作
- 往平衡树中插入一个大小为 $v$ 的节点。
只需要按照 $v$ 大小分裂成一棵 $val_x\le v$ 的平衡树 $T_x$ 以及一棵 $val_y>v$ 的平衡树 $T_y$,后合并 $T_x$ 与新节点,再将合并后的树与 $T_y$ 合并即可。注意合并顺序。
|
|
- 删除操作
- 删除平衡树中 一个 大小为 $v$ 的节点。
与上分裂相同,在分裂后的 $T_x$ 的再进行一次以 $v-1$ 为值分裂成 $T’_x$ 与 $T_z$,那么 $\forall z\in T_z,val_z=v$. 我们令 $z\gets\operatorname{merge}(ls_z,rs_z)$,根节点自然便被删除掉了。最后 按顺序 合并 $x,z,y$ 即可。
|
|
- 排名查询
- 查询 $\sum\limits_{x\in T}[val_x<v]+1$。
按照 $v-1$ 分裂成 $T_x$ 与 $T_y$,答案即为 $sz[T_x]+1$。最后记得合并回去。
|
|
- 查询第 $k$ 小的数
- 查询树中排名为 $k$ 的数。
从根节点不断递归,若 $sz[ls_R]+1=k$,那么 $val_R$ 即为答案;若 $sz[ls_R]+1<k$,那么答案在 $R$ 的右子树上,$k\gets k-(sz[ls_R]+1)$,并 $R\gets rs_R$;若 $sz[ls_R]+1> k$,那么答案在左子树上。
|
|
- 前驱查询
- 查询比 $v$ 小的最大数。
按照 $v$ 分裂为 $T_x$ 与 $T_y$,从 $x$ 不断向右子树递归,直到没有右子树停止,注意合并前保存答案,否则会被更改。
|
|
- 后继查询
- 查询比 $v$ 大的最小数。
按照 $v$ 分裂为 $T_x$ 与 $T_y$,从 $y$ 不断向左子树递归,直到没有左子树停止,注意合并前保存答案,否则会被更改。
|
|
了解完这些操作后,初学者理应理解了合并操作的 顺序 问题,同时也加深了对 分裂(split) 与 合并(merge) 操作的理解。
文艺平衡树
给出序列 $a={1,2,\cdots,n}$,进行 $m$ 次区间翻转操作,求操作进行完的序列。
我们前面提到了 按大小分裂 的形式,这道题很好的应用了这种分裂方式来维护序列。
尚未操作时,树的中序遍历显然是 $1,2\cdots,n$。考虑翻转操作怎么写。假设当前要翻转的区间为 $[l,r]$,那么根据平衡树的性质,我们从根节点按照树大小 $r$ 分裂出子树 $T_x$ 与 $T_z$,再以 $x$ 为根,大小为 $l-1$ 分裂出子树 $T’_x$ 与 $T_y$。为了增强初学者的理解,我们列出三棵子树所维护的区间:$T_x:[1,l-1],T_y:[l,r],T_z:[r+1,n]$(不考虑空集)。那么我们只需对 $T_y$ 进行操作即可。 我们是由中序遍历来得到答案的,那么必须要遍历完 $y$ 的左子树才能到 $y$,之后才是 $y$ 的右子树。这总体是一个 左根右 的 递归 过程。设代表的 $l$ 节点为 $i$,代表 $r$ 的节点为 $j$。遍历的过程中,我们只需要交换 $i$ 与 $j$ 便可交换序列中 $l$ 与 $r$ 的值。推广来说,我们只需要 递归 地交换 $ls_y$ 与 $rs_y$ 即可实现整段区间的翻转。可以从子树大小等多种角度理解这一过程,建议初学者画图来加深这一过程的理解。 但是,这样做的时间复杂度与直接暴力无异。我们类比线段树的 $tag$ 记号,在操作上打上 $tag$,并引入下传操作。时间复杂度便可期望地做到 $\mathcal O(n\log n)$。
|
|
P4146 序列终结者
维护长度为 $N$ 的序列 $a_n$,每次操作可以:给 $[l,r]$ 中每个数加上 $v$;翻转区间 $[l,r]$;查询 $\max\limits_{i\in[l,r]}a_i$。
给每个节点多加一个参数 $mx$ 表示最大值,类比线段树操作再加一个 $add$ 标记,代码与上题无异。
记得开 long long。
|
|
P3215 [HNOI2011] 括号修复 / [JSOI2011] 括号序列
动态查询修改一段串使其变为合法括号串的最小修改次数。
用到一个 Trick: 对于一个圆括号串 $s$ 我们设 $f(x)=\begin{cases}-1,& x=\texttt(\1,&x=\texttt)\end{cases}$, 对于区间 $s[l,r]$, $pre$ 表示关于 $f(x)$ 的前缀最大值,$suf$ 表示关于 $f(x)$ 的后缀最小值,那么使 $s$ 成为合法括号串的最小修改次数为 $\lceil\dfrac{pre}2\rceil+\lceil\dfrac{-suf}2\rceil$.
Proof 我们把所有已经匹配的括号删除,则剩下的串形如
))))...((..设右括号的数量为 $x$,左括号的数量为 $y$ 由于删除的串的贡献对于 $pre$ 与 $suf$ 来说必然是 $0$,那么 $pre=x$,$suf=-y$ 我们尝试设计一种方案来使其操作数最小 不妨考虑右括号。对于长度为 $x$ 的连续右括号来说,我们只需要将左侧 $\lfloor\dfrac{x}2\rfloor$ 变为右括号,就可以完全匹配。如果为奇数个,那么由于有解性,右侧的左括号必然为奇数个。这样只需要再多变换一个,即可完全匹配。因此对于右括号而言,答案为 $\lceil\dfrac{x}2\rceil$ 综上,答案为 $\lceil\dfrac{x}2\rceil+\lceil\dfrac{y}2\rceil=\lceil\dfrac{pre}2\rceil+\lceil\dfrac{-suf}2\rceil$
|
|