Tarjan 全家桶

2025-05-22T23:29:08+08:00 | 12分钟阅读 | 更新于 2025-05-22T23:29:08+08:00

@
Tarjan 全家桶

强连通分量、双连通分量以及圆方树。

Robert E. Tarjan（罗伯特·塔扬，1948~），生于美国加州波莫纳，计算机科学家。 Tarjan 发明了很多算法和数据结构。不少他发明的算法都以他的名字命名，以至于有时会让人混淆几种不同的算法。比如求各种连通分量的 Tarjan 算法，求 LCA（Lowest Common Ancestor，最近公共祖先）的 Tarjan 算法。并查集、Splay、Toptree 也是 Tarjan 发明的。 摘自 OI-Wiki

一、强连通分量

0、有向图的 DFS 生成树

(1) DFS 序

$u$ 的 DFS 序即为从某节点（根）开始遍历，首次到达 $u$ 的时间戳。

(2) 四条边

  1. 树边：DFS 树上的边。
  2. 返祖边：指向祖先节点的边。
  3. 前向边：指向子孙节点的边。
  4. 横叉边：指向的访问过的节点既不是自己的祖先节点也不是自己的子孙。

如下图，黑边为树边，绿边为返祖边，粉边为前向边，红边为横叉边。


图 $G$

$G$ 的 DFS 生成树

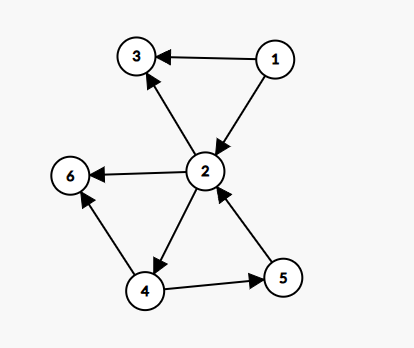
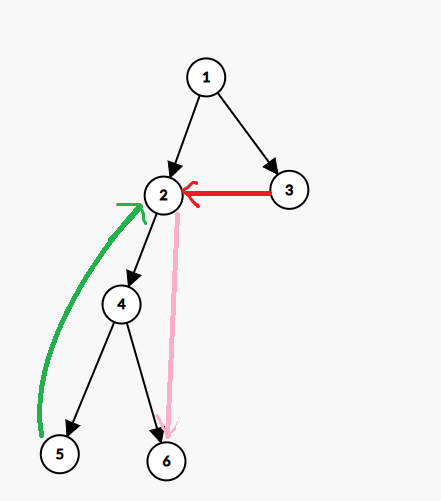
1. 基本概念

  • 强连通：在有向图 $G$ 中，任意两点联通。
  • 强连通分量（SCC）：有向图 $G$ 中，极大的强连通子图。对于“极大”，意思是这个子图无法再加入任意一点使其仍为强连通的。
  • SCC 的根：遍历这个 SCC 的第一个点

1.5 约定

  • $dfn_u$：遍历到 $u$ 的时间戳。
  • $low_u$：以 $u$ 为根的子树可以回溯到最早已经在栈中的节点的时间戳。

2. 求法

Trick

一个 SCC 的所有节点必定在其根的子树中。

我们于 dfs 过程中维护一个栈，里面是未处理的节点。

对于 $u$，我们枚举每一条 $u$ 出边 $(u,v)$。

  • 若 $v$ 未访问。我们向 $v$ 遍历，并更新 $low_u\gets\min(low_u,low_v)$。
  • 若 $v$ 已访问，且在栈内。$low_u\gets\min(low_u,dfn_v)$。
  • 若 $v$ 已访问，不在栈内。那么 $v$ 所在 SCC 已经处理完毕，不操作。

值得注意的是，有时在写强连通分量时，我们误将 $low_u\gets\min(low_u,dfn_v)$ 写作 $low_u\gets\min(low_u,low_v)$，虽然运行结果正确。然而这实际上不符合我们推导以及思考过程，在求双连通分量中这样是错误的。因此需要注意这个问题。

对于一个 SCC，有且仅有一个点使得 $low_u=dfn_u$。

简证

存在性：假设 SCC 根节点为 $R$，那么必然有 $dfn_R=low_R$。这是因为如若 $low_R < dfn_R$，那么说明存在点 $v$ 使 $v$ 加入当前 SCC 点集后仍然是一个 SCC，与定义“极大的”矛盾。

唯一性：除根节点外的所有子节点，必有 $low_u< dfn_u$。这是由于所有子节点都可以回溯到时间戳早于它的节点。

我们只需找到这样的点，将这个点以及栈内所有晚于这个点入栈的点弹出，所构成的即为一个 SCC。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

void tarjan (int x) {
    dfn[x] = low[x] = ++ tim;
    inst[x] = true;
    st.push (x);

    for (auto to : e[x]) {
        if (!dfn[to]) tarjan (to), low[x] = min (low[x], low[to]);
        else if (inst[to]) low[x] = min (low[x], dfn[to]);
    }

    if (dfn[x] == low[x]) {
        int tp;
        ans.push_back ({});
        do {
            tp = st.top (); st.pop ();
            ans.back ().push_back (tp);
            id[tp] = ans.size ();
            inst[tp] = false;
        } while (tp != x);
    }
}

这整个过程的时间复杂度非常优秀，为 $\mathcal O(n+m)$。

3. 例题

P3387 【模板】缩点

模板题。 我们可以发现，在经过缩点操作后的新图是一个有向无环图，故可以在新图上进行 DP 操作。

P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G

对原图缩点后，原图中属于出度为 $0$ 的那个点的所有点即为答案。

P2812 校园网络【[USACO]Network of Schools加强版】

缩点，第一个答案为新图入度为 $0$ 点的个数，第二个答案为入度为 $0$ 点个数与出度为 $0$ 点个数的最大值。

P4306 [JSOI2010] 连通数

缩点后建反图，拓扑 DP 即可。 另解：用 bitset 优化的传递闭包。

P2272 [ZJOI2007] 最大半连通子图

原图上是存在环的，所以我们先缩点，得到一张 DAG。根据半连通的定义，我们从入度为 $0$ 的点开始 DP。设 $c_i$ 表示 SCC $i$ 所含节点数，$f_i$ 表示到 $i$ 的最大半连通子图节点数，$g_i$ 表示方案数。那么对于边 $(u,v)$，$f_v\gets \max(f_v,f_u+c_v)$，$g_v\gets\begin{cases}g_u,& f_v<f_u+c_v\g_u+g_v,&f_v=f_u+c_i\end{cases}$。

二、双联通分量，割点与桥

0. 无向图的 DFS 生成树

这部分十分简单，图上边分为树边与非树边。顾名思义。

1. 基本概念

  • 割点：无向连通图 $G$ 中，若删除 $u$ 使得 $G$ 不再连通，那么 $u$ 就是 $G$ 的一个割点。
  • 桥（割边）：无向连通图 $G$ 中，若删除边 $e$ 使得 $G$ 不再连通，那么 $e$ 就是 $G$ 的一个桥。
  • 边双连通：若无向连通图 $G$ 不存在桥，那么 $G$ 就是边双连通的。
  • 点双连通：若无向连通图 $G$ 不存在割点，那么 $G$ 就是点双连通的。
  • 边双连通分量：若 $G’$ 是无向图 $G$ 的 极大 的边双联通子图，那么 $G’$ 就是 $G$ 的一个边双连通分量。下文简称为“边双”。
  • 点双连通分量：若 $G’$ 是无向图 $G$ 的 极大 的点双联通子图，那么 $G’$ 就是 $G$ 的一个点双连通分量。下文简称为“点双”。

这里的“极大”与强连通分量中含义一致。

1.5 约定

  • $dfn_u$：遍历到 $u$ 的时间戳。
  • $low_u$：以 $u$ 为根的子树通过非树边可到达的最小时间戳。
  • $subtree_u$：以 $u$ 为根的子树。

2. 割点 & 点双联通分量

(1) 求割点

类似的，我们考虑 $dfn$ 与 $low$ 的关系。 对于点 $u$ ，若存在 $v\in subtree_u$ 使得 $low_v\ge dfn_u$，也就是说 $v$ 无法通过非树边到达 $u$ 的祖先，那么 $u$ 即为一个割点。特别的，当 $u$ 为搜索起始点时，若其仅有一个子节点，那么删除 $u$ 并不会增加图的连通子图数，因此并不会成为割点；反之，若其多于一个子节点，那么其必然为割点。

简证 命题：$\exist v\in subtree_u,low_v\ge dfn_u\iff u$ 是割点。

若 $v\in subtree_u$，那么 $v$ 是第一次被遍历，且由 $u$ 而来。且对于其到达不在根到 $u$ 路径上的节点的非树边，到达的时间戳必然是大于其本身的。因此当 $low_v\ge dfn_u$ 时，$v$ 必然无法通过非树边到达 $u$ 的祖先。 如若存在这样的 $v$，但 $u$ 不是割点。由于 $v$ 无法通过非树边到达 $u$ 的祖先，故 $v$ 必须通过 $u$ 到达其余点，因此 $u$ 必然为割点。故充分性成立。 如若 $u$ 为割点，假设不存在这样的 $v$：那么所有 $v$ 必然经过 $u$ 到达小于 $low_u$ 的点。然而根据 dfs 的性质，我们发现连接 $u$ 的非树边的 $dfn$ 值是必然大于 $u$ 的，同样的，向上遍历亦如此。故必要性成立。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

void tarjan (int x, int root) {
    dfn[x] = low[x] = ++ tim;
    int son = 0;
    for (auto to : g[x]) {
        if (!dfn[to]) {
            tarjan (to, root);
            low[x] = min (low[x], low[to]);
            if (x != root && low[to] >= dfn[x]) cut[x] = true;
            if (x == root) ++ son;
        }  else low[x] = min (low[x], dfn[to]);
    }
    if (x == root && son >= 2) cut[x] = true;
    ans += cut[x];
}

(2) 求点双连通分量

由于点双中不存在割点，因此我们类比求割点的做法，就可以推出点双的做法。 同样的，我们维护一个栈。对于 $u$，我们如果枚举到了 $v$ 使得 $low_v\ge dfn_u$，那么 $u$ 即为割点。并不断弹出栈内元素直至栈顶为 $u$，这些部分构成一个点双。值得注意的，对于根节点，如若没有子树，则它就单独构成一个点双；如若有多个子树，那么就是一个割点；如若只有一个子树，那么他就是所在点双的根。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

void tarjan (int x, int root) {
    dfn[x] = low[x] = ++ tim;
    st.push (x);

    int son = 0;
    for (auto to : e[x]) {
        if (!dfn[to]) {
            ++ son;
            tarjan (to, root);
            low[x] = min (low[x], low[to]);
            if (low[to] >= dfn[x] ) {
                int tp;
                ans.push_back ({});
                do {
                    tp = st.top (); st.pop ();
                    ans.back ().push_back (tp);
                } while (tp != to);
                ans.back ().push_back (x);
            }
        } else low[x] = min (low[x], dfn[to]);
    }
    if (root == x && !son) {
        ans.push_back ({});
        ans.back ().push_back (x);
        return ;
    }
}

3. 桥 & 边双连通分量

(1) 桥

我们只需将割点的判定条件改为 $low_v>dfn_u$ 即可。证明与上类似。值得注意的是，若 $(u,v)$ 仅有一条边时为桥，多于一条边时，需要特殊判定。若 $v$ 多次枚举到 $u$，那么不为桥。我们只需加上特判即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

void tarjan (int u, int fa) {
	dfn[u] = low[u] = ++ tim;
	bool flag = false;
	for (int i = head[u]; i; i = nxt[i]]) {
		int v = to[i];
		if (!dfn[v]) {
			tarjan (v, u);
			low[u] = min (low[v], low[u]);
			if (low[v] > dfn[u]) isbridge[i] = isbridge[i ^ 1] = true;
		} else {
			if (flag || v != fa) low[u] = min (low[u], dfn[v]);
			else flag = true;
		}
	}
}

(2) 边双连通分量

我们先把所有桥求出，后再次进行 dfs。具体的，我们枚举每个未被枚举的点 $u$，从 $u$ 开始搜索，将所有不经过桥所连点加入当前的边双集合。这样就得到了全体的边双集合。

1
2
3
4
5
6
7
8
9

void dfs (int x) {
	E_BCC[id].push_back (x);
	vis[x] = id;
	for (int i = head[x]; i; i = nxt[i]) {
		int v = to[i];
		if (vis[v] || isbridge[i]) continue;
		dfs (v);
	}
}

实际上也有另一种简便的求法，与求强连通分量的过程十分相似（实际上一致）。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

void tarjan (int u, int id) {
    dfn[u] = low[u] = ++ tim; 
    st[++ tp] = u; inst[u] = true;
    for (int i = head[u]; i; i = e[i].nxt) {
        if (i == (id ^ 1)) continue;
        int v = e[i].v;
        if (!dfn[v]) tarjan (v, i), low[u] = min (low[u], low[v]);
        else if (inst[v])           low[u] = min (low[u], dfn[v]);
    }
    if (dfn[u] == low[u]) {
        ++ coll;
        do {
            col[ st[tp] ] = coll;  
            inst[ st[tp] ] = false;
        } while (st[tp --] != u);
    }   
}

4. 例题

P8435 【模板】点双连通分量 & P8436 【模板】边双连通分量 & P3388 【模板】割点（割顶）

模板题。

P3225 [HNOI2012] 矿场搭建

我们对每一个点双讨论：

  1. 若当前点双不存在割点，则这个点双不与外界相连，因此只能从其本身逃出。那么至少需要两个出口（防止其中之一被炸了）。
  2. 若当前点双存在一个割点，割点可能会被炸，因此我们还需要再这个点双内放置一个出口。
  3. 若当前点双存在不少于两个割点，那么任意一个点爆炸都可以从其他割点逃出。因此无需放置。

那么做法就十分显然了。设出口数为 $cnt$，方案数为 $ans$，当前点双的点数为 $n$。对于度数为 $0$ 的点双，$cnt\gets cnt+2$，$ans\gets ans\times n\times (n-1)\times\dfrac12$。对于度数为 $1$ 的点双，$cnt\gets cnt+1$，$ans\gets ans\times (n-1)$（根据前面的讨论，割点是不能当作出口的）。对于其他度数的点双，我们无需统计。

P8867 [NOIP2022] 建造军营

首先进行边双缩点，后形成一个树结构，两点之间的连边为桥。考虑树形 DP。

圆方树

仙人掌

一条边至多在一个环内的无向连通图。

构建

对于所有环，建立虚点——「方点」。对于环上点，称为「圆点」。

在新图中，对于不在同一个环中的圆点，继承原图中的连边关系。对于环上的所有圆点，向方点连边。于是新图的所有边分成了「圆圆边」、「圆方边」。

实际上，这是一种「边双建图」的方式。故含「圆圆边」。

特别的，在广义圆方树（即一般图的圆方树）中，采用的是点双建图。仅含圆方边。

example

关于代码，由于广义圆方树包含这种情况，所以就不特地写仙人掌圆方树的代码了。详细见下文的一般图圆方树代码。

例题

P5236 【模板】静态仙人掌

给出有边权的仙人掌，多次询问点对最短路。

$n,q\le 10000,m\le 20000$。

$w\le 10^5$。

按照上述过程建立圆方树，考虑如何对两点求出距离，即对新图边的赋值问题。

对于圆圆边， 显然按照原图权值分配即可。故只需考虑对于圆方边的刻画。

不妨任意选一圆点为根。由于仙人掌的性质，一个环上的点的深度呈现 $d,d+1,d+1\cdots,d+1$。取深度最小的点，称之为该环的根。每个点到方点的边权就是点到根的最小距离。

由于仙人掌的良好性质，一个环仅有一条返祖边。维护环上点通过返祖边或者不通过返祖边到达根的距离。

在查询时，直接查询到 LCA 的距离之和。若 LCA 为方点，考虑在 LCA 处的最小路径即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

#include <array>
#include <vector>
#include <iostream>

using namespace std;

const int N = 20010;

int n, m, q;
vector < pair <int, int> > g[N], ng[N];
int dfn[N], low[N], tim, cnt;
int st[N], tp, d[N], backd[N], upd[N], up[N];
int fa[N][16], dep[N], nd[N], len[N];
int counterrr[N];

void tarjan (int u) {
    dfn[u] = low[u] = ++ tim;
    st[++ tp] = u; int now = u;
    for (const auto& [v, w] : g[u])
        if (!dfn[v]) {
            d[v] = d[u] + w;
            up[v] = w;
            backd[v] = w;
            tarjan (v);
            low[u] = min (low[u], low[v]);
            if (dfn[u] == low[v]) {
                ++ cnt;
                int bck = backd[st[tp]], upp = d[st[tp]] - d[u];
                do {
                    int u = st[tp];
                    backd[u] = bck; upd[u] = upp;
                    bck += up[u]; upp -= up[u];
                    ng[u].emplace_back (cnt, min (backd[u], upd[u]));
                    ng[cnt].emplace_back (u, min (backd[u], upd[u]));
                } while (st[tp --] != v);
                ng[u].emplace_back (cnt, 0);
                ng[cnt].emplace_back (u, 0);
            }
        }
        else if (dfn[v] < dfn[u]) { low[u] = min (low[u], dfn[v]); if (w != up[u]) backd[u] = w; }
}

void dfs (int u) {
    dep[u] = dep[fa[u][0]] + 1;
    for (int i = 1; i <= 15; i ++) fa[u][i] = fa[fa[u][i - 1]][i - 1];
    for (const auto& [v, w] : ng[u]) {
        if (v == fa[u][0]) continue;
        fa[v][0] = u;
        nd[v] = nd[u] + w;
        dfs (v);
    }
}

array <int, 3> lca (int u, int v) {
    if (dep[u] < dep[v]) swap (u, v);
    for (int i = 15; ~i; i --)
        if (dep[fa[u][i]] >= dep[v]) u = fa[u][i];
    if (u == v) return {u, 0, 0};
    for (int i = 15; ~i; i --) 
        if (fa[u][i] != fa[v][i])
            u = fa[u][i], v = fa[v][i];
    return {fa[u][0], u, v};
}

int getmin (int u, int v) {
    if (upd[u] < upd[v]) swap (u, v);
    return min (backd[u] + upd[v], upd[u] - upd[v]);
}

int main (void) {

    scanf ("%d%d%d", &n, &m, &q); cnt = n;
    for (int i = 1; i <= m; i ++) { 
        int u, v, w; scanf ("%d%d%d", &u, &v, &w);
        g[u].emplace_back (v, w);
        g[v].emplace_back (u, w);
    }

    tarjan (1);
    dfs (1);
    while (q --) {
        int u, v; scanf ("%d%d", &u, &v);
        const auto [_lc, a, b] = lca (u, v);
        if (_lc > n) printf ("%d\n", nd[u] - nd[a] + nd[v] - nd[b] + getmin (a, b));
        else    printf ("%d\n", nd[u] + nd[v] - nd[_lc] * 2);
    }

    return 0;
}

P4630 [APIO2018] 铁人两项

给出无向连通图，求 $s\to c\to f$ 为简单路径的有序点对数。

$n\le10^5,m\le2\times10^5$。

这里其实可以讲一个点双的性质。

性质

  • 一个点双中 $u,v$ 的简单路径的并集为整个点双。

这是一个十分良好的性质。可以推广出在整个图中，固定 $s,f$ 后，所有合法的 $c$ 为 $s\to f$ 在圆方树上的简单路径上，经过所有点双的并减二（不能选自己）。

下面就是对圆方点赋值问题。由于仅圆方点是交替的，故在路径上（不包括 $s,f$）每个圆点都会在两个方点之中。因此对所有圆点赋值 $-1$，方点赋值为所在点双大小，这样就可以直接求出二者之间的 $c$ 的数量。设点的权为 $w_i$。

然而这个做法是 $\mathcal O(n^2)$ 的，考虑优化。

设 $f(u)$ 表示 $u$ 作为 $c$ 的 $s,f$ 点对个数，$sz_u$ 表示以 $u$ 为根的子树中圆点数量。讨论 $u$ 为方点还是圆点。

  • 对于方点，考虑两两子树圆点配对，以及以当前为根的子树与整棵去掉该子树的树上圆点的配对。即 $2w_u\times [\sum\limits_{w,v\in son_u} siz_w\times siz_v+(siz_{rt}-siz_{u})\times siz_u]$。
  • 对于圆点，根据上文所言，直接容斥掉重复部分。与上转移式相同。

如果对于圆点的容斥不太清楚，可以考虑每次「配对」实际上是枚举 $s,f$ 的过程。对于每个 $u$ 都确定了互不相同的多个点对。考虑把这个东西看作固定 $s,f$ 求 $c$ 数量，显然由于圆方间隔这个容斥是对的，这就说明一组点对只会被两个方点重复统计。因此统计到圆点直接减掉经过其的所有点对就是对的，这两者转化之间是一一映射的。

P4606 [SDOI2018] 战略游戏

给出无向连通图。多次询问，每次询问给出点集 $S$。求点集内任意两点路径上割点数量之和。

$\vert S\vert\le 2\times10^5$。

把圆方树建出来，问题转化为求任意两点简单路径圆点并集大小。朴素的方法是 $\mathcal O(n^2)$ 的，考虑如何刻画并集这一过程。

发现实际上只要求任意二者之间的 LCA 后求并。考虑 DFS 的遍历过程，对于先后遍历顺序相邻两个关键点，DFS 的过程实际上就是在图上「行走」，且每个点至多被经过两次。将点按照 DFS 序排序后，相邻两点就是 DFS 序的遍历过程。因此，被经历过点的个数就是相邻（首尾算相邻）两点路径和的一半。

计算圆点个数是 $d(u)+d(v)-2d(lca)$，这是因为 $lca$ 会被计算包含，不能被重复计算。

过程是进出两次，故对路径之和取一半。注意首尾 LCA 圆点没被计算，算进去即可。

© 2025 - 2026 Toorean's Blog

🌱 Powered by Hugo with theme Dream.

About Me

来自安徽合肥，目前在合肥市第一中学读高中。

弱小的 OIer，或许就要退役了呢？

QQ: 3427463298 Email: phantomxbee@outlook.com